Readings

This is an implementation of the “hash array mapped trie,” a purely functional hashmap. In an ordinary trie hashmap, the keys are stored as bitstrings in a trie, as follows:

   0
  / \
  1 0
/ \ / \
1 0 1 0 
| | | |
X F D E

This saves space compared to a traditional Hashmap, and it means resizings are never necessary.

The HAMT improves on this by instead storing in each node a table with N (32 with 32-bit words) entries, with each entry containing a pointer to another node. When traversing or inserting a key, you consider the most significant T=log_2(N)=5 bits of the hash; this indexes to either a submap, a value, or nil. It starts out as a value, then a submap is added when a new hash collides with an existing one. This submap then behaves like the root map, but with the next 5 bits of the hash as a key. With T=2:

00 01 10 11
|   |  |  |
|   G     O
|
00 01 10 11
|  |  |  |
E     D

This means that lookup time is reduced to log_N(n) from log_2(n), without taking up much additional space.

Another note: to save space in the tables, only the keys that point to actual values or nodes are represented. This is done by adding an N-bit bitmap to each node, with the ith bit representing whether that pointer is nil. Then, the index into the table is found by calculating the hamming weight (number of 1s) in the first i bits of the bitmap, where i is also the T-bit key into the subtable.

// Modified above example
bitmap: 1101
0 1 2
| | |
| G O
|
...

This means that the table must be resized every time a new key is inserted. Still, the immutable version is significantly slower than the equivalent mutable version, by a factor of about 10 with 1000 inserts.

test hashmap_insert_10         ... bench:       5,991 ns/iter (+/- 185)
test hashmap_insert_100        ... bench:     197,136 ns/iter (+/- 9,000)
test hashmap_insert_1000       ... bench:   2,990,670 ns/iter (+/- 133,638)
test hashmap_insert_mut_10     ... bench:       1,961 ns/iter (+/- 191)
test hashmap_insert_mut_100    ... bench:      29,460 ns/iter (+/- 2,971)
test hashmap_insert_mut_1000   ... bench:     305,106 ns/iter (+/- 17,927)

The 100 prisoners problem is a probability thought exercise with an unintuitive solution, kind of like the Monty-Hall problem. The setup is this: there are 100 numbers in drawers, each corresponding to one of 100 prisoners. Each prisoner is allowed to pick 50 drawers, but the drawers are reset after each prisoner makes their choice (and there’s no communication between prisoners). The goal is for each prisoner to find their number – if that happens, they escape their sentence.

The naive solution is to pick the 50 drawers at random, giving each prisoner a 50% chance of success (and a vanishingly small chance – .50^100 – for all 100 prisoners to pick the correct number). But there’s a strategy that drastically improves the odds of success, bringing it to ~30%.

This strategy does not appear much different from the naive one, but it relies on the hidden correlation between success and failure in the permutation cycles to shape the search space. Namely, the prisoners want to search a set that’s as different as possible from everyone else’s – since they know the world where they succeed is one in which they all pick different boxes.

The the Monty Hall-inspired analogy on the Wikipedia page gives a good explanation of this. Essentially, the contestants choose doors (over two rounds) in a way that they’re never picking the same door in the same round.

Consider how the prisoners could design their choices similarly. If, in the case where each prisoner is only allowed to search a single box, all prisoners just choose box 1, there is no possibility of success: Only one prisoner will find the correct number. Choosing a box at random has some probability of success, if extremely low: 100^-100. If instead each prisoner i chooses the ith box, the chances are improved: it’s now 1/(100!), since each correctly chosen box constrains the options for future boxes. If just you expand that search to the next 50 boxes, you still don’t get the optimal solution - starting with a ¹⁄₂ chance of success for the first prisoner, the next 50 prisoners slowly widdle that down to 1 (the resulting probability is 50^50/(100!/50!)).

It follows along these lines that permutation cycles, being disjoint, are better for structuring the search. But I’m not sure how to make this intuition concrete, if that’s even possible.

I found Urbit when somebody compared it to the “decentralized Internet” that Silicon Valley’s Pied Piper is building. It turns out that it’s even more ambitious than that – an attempt to rebuild the whole software stack from the Kernel up – but this summary will focus on the network part.

This paper is an overview of synchronization methods across the hardware stack, with an analysis that attributes high-level performance differences to low-level hardware constraints.

Among the key takeaways:

Latency of atomic operations: There is a heavy penalty for cross-socket sharing - ie, passing data between cores (or hyperthreads). This outweighs other sources of latency by far.

Locking vs message passing: Message passing is better when data has high contention, locking with low contention.

Performance of different types of locks: Each of the nine locks considered is the best performer in certain situations. The ticket lock is the best performer in most low-contention cases, though–the “ticket lock” being a spinlock that uses a FIFO queue to determine which thread is allowed to proceed.

Here are some highlights for the Hacker News AMA of Alan Kay, pioneering researcher in graphical user interfaces and object-oriented programming.

Part of this was that the rather good idea of parsing non-command messages in each process – we used this in the first Smalltalk at Parc – became much too ad hoc because there was not a strong attempt to intertwine a real language around the message structures (this very same thing happened with http – just think of what this could have been if anyone had been noticing

Mr. Kay thinks that current message-passing protocols (like HTTP or Unix process communication) don’t stand up well to the formal treatment of message-passing in Smalltalk. As background, Smalltalk’s message handling was done by dynamic dispatch on objects. This would allow inheritance of message handling, so that, eg, the default implementation was to return messageNotUnderstood.¹ There is perhaps also the advantage that message fields are parsed by the language parser, making it an actual component of the language that might allow, eg, for easier static analysis. I’m only speculating on the specifics, though, since Mr. Kay doesn’t make this part clear.

– I was surprised that the HN list page didn’t automatically refresh in my browser (seems as though it should be live and not have to be prompted …)

Mr. Kay comments earlier on the “worse is better” vs “better is better” approaches to user interface design, but this, I think, is a better, more concrete way of answering the question. Hacker News is itself an embodiment of “worse is better”, avoiding new features and maintaining what one commenter points out is an “old school” feel. Mr. Kay counters with an interesting critique, saying that if old school means how things were done, eg, at PARC, that’s more than this website can do! That’s to say that old school software was often more capable than we give it credit for, not static, as we often imagine it, but experimenting with new modes of interaction just like fast-moving software today. We shouldn’t, therefore, fold up new features simply because they wouldn’t be “old school” enough, as if the researchers at PARC and Bell Labs achieved the perfect form of computing.

Roofnet is a WiFi mesh network for increasing Internet access in urban areas. It’s designed to be easy to set up: Users just need to place antennae on their roofs, and there’s no need surveys to determine the optimum place to put them – since the network makes up the difference in performance. It does that, in part, though its routing protocol, which chooses routes that maximize bitrate and minimize loss-rate. It also introduces a new protocol that maximizes throughput no matter the loss rate – transmitting at a lower bitrate can improve performance by avoiding re-transmissions, and this protocol improves on the heuristics used by its predecessors (although not described in detail here).

In summary: Some number of nodes in the network have wired access to the Internet. The rest of the nodes need to route their packets to these gateway nodes, with some number of hops. Roofnet does that without much performance loss by choosing the highest-throughput routes, using multiple links if necessary.

Magic Pocket is Dropbox’s distributed storage system. It prioritizes simplicity, durability and availability, with a multi-level design that uses centralized coordination where possible. Data is replicated on all levels: between zones (which span an entire region, like the Eastern US) but also within each zone. The author notes in a HN comment the high-level similarities with GFS, which may warrant a closer look.

Below the level of zone is the cell, the largest storage unit with central coordination. The cell contains volumes, which are replicated over several physical storage units, or OSDs. The cell’s master controls tasks like the creation and deletion of buckets, and repair of volumes in case of OSD failure. The data flow of the cell works independently of the master, though: a separate replication table maps buckets to physical storage locations, keeping it working in case of failure of the master. The master’s protocol ensures consistency in the event of failure or restart of any component, notably by storing the generation of each volume-to-OSD mapping with the volume and in the replication table. Eg, if the master hangs in the middle of a repair process and later comes back to life, it will not try to continue that repair (or will at least not leave the system inconsistent - the exact mechanism that prevents that is unclear).

Some other characteristics: the smallest units of file storage are immutable, like git’s or IPFS’s: changes are written to a journal and each change creates a new block. This prevents inconsistency that could result from updating some copies of the file but not others. It’s also optimizing for temporal locality – files that get changed are the most likely to get changed again soon – while making sure that even old files can be accessed quickly. It does this, per the author’s comment on HN, by applying the above replication scheme for 24 hours after a volume is created. After that, data is replicated by a more efficient erasure-coding system.

In another interesting HN comment, the author points out that the blocks are actual blocks on the storage device, directly managed without any intermediate filesystem.

The skip list is an alternative to balanced search trees, especially suited for distributed applications. MemSQL is the main adopter, using skip lists as its primary index structure, but they’re also used in Redis to implement ordered sets.

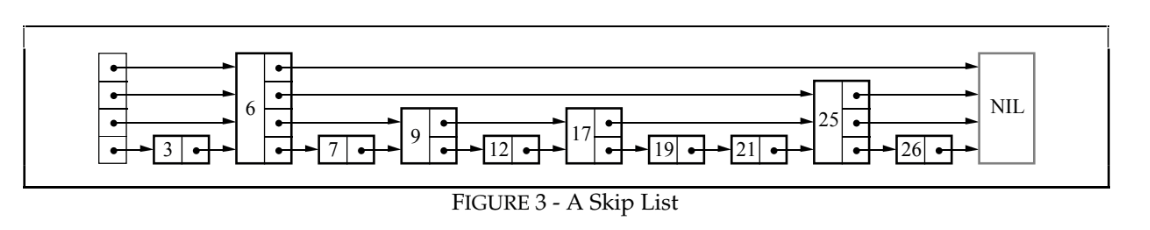This image from the paper shows what the data structure looks like. A node contains k pointers, with the ith pointer pointing to the next node of level i: When a node is inserted, it is given a random level to represent it: level 1 with 50% probability, 2 with 25%, etc. Searches are started at the top level, with each node acting as an index to the lower level. This process is like a binary search – if the skip list is balanced, the search traverses only 1-2 nodes at each level.

The paper defends the claims that 1) concurrency guarantees are easier to implement for skip lists than for balanced trees, requiring only write locks on the nodes being written, and 2) the data structure is very unlikely to become significantly unbalanced. With skip lists having the advantage of 1) and having similar performance to balanced trees, they appear to provide an advantage in concurrent applications.

To ensure that readers are not disrupted by writes in the absence of read locks, x is updated to point to its predecessor after removing x. Proofs are supplied for the correctness guarantees, among them that the list remains sorted and the lock is held only by the deleted key.

Although the worst case search time is O(n), in the case, for example, that the only node at each level i is the first node in the list at level 0, this is an unlikely outcome. The probability distribution over the comparisons required is similar to that of the number of coin flips needed to see k heads, where k is equal to the number of levels. Showing that distribution is apparently left by the authors as an exercise for the reader, but it makes intuitive sense: the most likely outcome is 1-2 comparisons on each level, corresponding to the most likely outcomes of 1 or 2 coin flips needed to see 1 head.

This is a pretty neat showcase about customizing the touchbar on the latest Macbook Pros. It’s appropriate that it begins with a picture of the author’s super customized Linux desktop from 2007, because the last time I thought about this sort of thing was while reading “show off your desktop” threads in Macrumors threads c. 2007-2008. I wasn’t aware that Applescript was so capable – it has super convient APIs for apps like Spotify and concise JSON fetching and parsing.

It sort of makes me want to get a MBP, even though my impressions of it have soured because of the constant negativity about it on Hacker News and elsewhere.

This is an interesting – paraphrasing from the article – “distillation of reinforcement learning research from the past two decades,” approaching from a cognitive science perspective. It considers the paradigm of training a large (many parameter) model to build a representation of the environment and its future, then training a smaller controller model, which outputs actions, from that representation. The future model, they argue, is similar to the way that humans make decisions – by considering how their actions will affect the future.

The RNN part of the model uses an approach similar to the one that SketchRNN does to predict future actions. It sends compressed version of the environment through a feed-forward RNN, taking, at each stage t, the hidden vector h{t-1}, the action a{t-1}, and an additional input z_{t-1}. z_t is a vector sampled from the mixture of Gaussian distributions output by a Mixture Density Network.

These actions are generated by the final layer of the model, the controller, which takes h_t and z_t as input.

They conduct a variety of experiments using various combinations of the three layers, showing, eg, that the full model is better than just using the RNN as input to the controller.

What’s interesting is that they can use the VAE to decode the latent vectors in the MDN-RNN model, giving a representation of the model’s prediction of the future environment. After training the model only to learn this virtual representation, they can then train the M and C layers on it and apply it to the real environment.